不久之前看了「编程之美」,里面有在windows下操纵CPU绘制正弦曲线的示例程序。思路很简单,但是需要知道几个windows的API函数。 刚开始我想尝试在windows下绘制心形,不过没能做到,原因是CPU曲线是CPU利用率和时间构成的函数的关系,心形是一个封闭图形,不可能是一个函数,所以至少需要两条CPU曲线才能绘制(这需要你的机器为双核或多核或者多个CPU),然而windows的任务管理器,我没能找到将两条CPU曲线绘制在同一图表下的方法,所以没能成功。 不过ubuntu下的任务管理器可以,而且还可以设置CPU曲线的颜色。以下是我在ubuntu下任务管理器的截图,我把两条CPU曲线都设置成了红色,设置CPU曲线的刷新速率为2s。
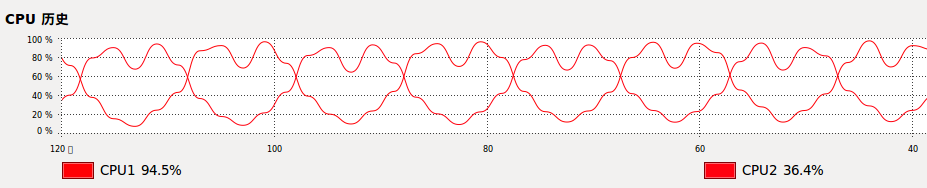
绘制正弦曲线的程序思路很简单,在看过「编程之美」后,完全可以仿照写出Linux版本,只是引用的库和调用的API函数不通而已。书中没有双核的参考程序,要让特定的线程在特定的cpu上运行需要设置cpu亲和度,windows下可参考这篇博客 http://blog.csdn.net/wesweeky/article/details/6402564
我本来想用经典的心形曲线X^2+(y-(x^2)^(1/3))^2=1来绘制,但是效果不是很好,所以干脆使用几个分段的二次函数。详细代码如下:
/*Programmed by Wang Zaijing 2011-08-01*/
#include <stdio.h>
#include <pthread.h>
#include <unistd.h>
#include <stdlib.h>
#include <math.h>
#include <time.h>
#include <sys/time.h>
#define SAMPLE_COUNT 800 //设置800个抽样点
#define INCREAMENT 0.0025 //增量为0.0025=2/800
#define SAMPLE_TIME 25 //设置每个抽样点的时间片
double GetSysTime() //Windows中直接使用GetTickSAMPLE_COUNT()函数./ms
{
struct timeval tv;
gettimeofday(&tv, NULL);
return (tv.tv_sec*1000+tv.tv_usec*1.0/1000);
}
int GetCpuNums()
{
return (int)sysconf(_SC_NPROCESSORS_ONLN);
}
void *thread_cpu1(void*arg) //线程函数1
{
double busy_cache[SAMPLE_COUNT]; //CPU占用时间,缓存一个周期的计算结果
double idle_cache[SAMPLE_COUNT]; //CPU空闲时间
double radian = 0.0; //增量从0开始,最大值到2=SAMPLE_COUNT*INCREAMENT
double start_time; //开始时间
double temp;
//一个周期内为分段函数分为四段
for(int i=0; i<SAMPLE_COUNT/4; i++)
{
temp = (double)(-8.0*(radian-0.25)*(radian-0.25)+1);
busy_cache[i] = (double)(SAMPLE_TIME*temp);
idle_cache[i] = (double)(SAMPLE_TIME - busy_cache[i]);
radian += INCREAMENT;
}
for(int i=SAMPLE_COUNT/4; i<SAMPLE_COUNT/2; i++)
{
temp = (double)(-8.0*(radian-0.75)*(radian-0.75)+1);
busy_cache[i] = (double)(SAMPLE_TIME*temp);
idle_cache[i] = (double)(SAMPLE_TIME - busy_cache[i]);
radian += INCREAMENT;
}
for(int i= SAMPLE_COUNT/2; i < 3*SAMPLE_COUNT/4; i++)
{
temp = (double)(0.667*(radian-2)*(radian-2)-0.167);
busy_cache[i] = (double)(SAMPLE_TIME*temp);
idle_cache[i] = (double)(SAMPLE_TIME - busy_cache[i]);
radian += INCREAMENT;
}
for(int i= 3*SAMPLE_COUNT/4; i < SAMPLE_COUNT; i++)
{
temp = (double)(0.667*(radian-1)*(radian-1)-0.167);
busy_cache[i] = (double)(SAMPLE_TIME*temp);
idle_cache[i] = (double)(SAMPLE_TIME - busy_cache[i]);
radian += INCREAMENT;
}
for(int i = 0; ; i = (i + 1) % SAMPLE_COUNT)
{
start_time = GetSysTime();
while((GetSysTime()-start_time) <= busy_cache[i]);
usleep(idle_cache[i]*1000);
}
return NULL;
}
void *thread_cpu2(void*arg)//线程函数2,原理同线程函数1
{
double busy_cache[SAMPLE_COUNT];
double idle_cache[SAMPLE_COUNT];
double radian = 0.0;
double start_time;
double temp;
for(int i=0; i<SAMPLE_COUNT/4; i++)
{
temp = (double)(0.667*(radian-1)*(radian-1)-0.167);
busy_cache[i] = (double)(SAMPLE_TIME*temp);
idle_cache[i] = (double)(SAMPLE_TIME - busy_cache[i]);
radian += INCREAMENT;
}
for(int i= SAMPLE_COUNT/4; i < SAMPLE_COUNT/2; i++)
{
temp = (double)(0.667*(radian)*(radian)-0.167);
busy_cache[i] = (double)(SAMPLE_TIME*temp);
idle_cache[i] = (double)(SAMPLE_TIME - busy_cache[i]);
radian += INCREAMENT;
}
for(int i=SAMPLE_COUNT/2; i<3*SAMPLE_COUNT/4; i++)
{
temp = (double)(-8.0*(radian-1.25)*(radian-1.25)+1);
busy_cache[i] = (double)(SAMPLE_TIME*temp);
idle_cache[i] = (double)(SAMPLE_TIME - busy_cache[i]);
radian += INCREAMENT;
}
for(int i=3*SAMPLE_COUNT/4; i<SAMPLE_COUNT; i++)
{
temp = (double)(-8.0*(radian-1.75)*(radian-1.75)+1);
busy_cache[i] = (double)(SAMPLE_TIME*temp);
idle_cache[i] = (double)(SAMPLE_TIME - busy_cache[i]);
radian += INCREAMENT;
}
for(int i = 0; ; i = (i + 1) % SAMPLE_COUNT)
{
start_time = GetSysTime();
while((GetSysTime()-start_time) <= busy_cache[i]);
usleep(idle_cache[i]*1000);
}
return NULL;
}
int main()//主函数
{
//int cpu_num = 0;
//cpu_num = GetCpuNums();
//printf("The number of cpu is %d\n", cpu_num);
pthread_t t1;
pthread_t t2;
pthread_attr_t attr1;
pthread_attr_t attr2;
pthread_attr_init(&attr1);
pthread_attr_init(&attr2);
if (0!=pthread_create(&t1, &attr1, thread_cpu1, NULL))//创建线程1
{
printf("error:Create thread 1\n");
return 0;
}
if (0!=pthread_create(&t2, &attr2, thread_cpu2, NULL))//创建线程2
{
printf("error:Create thread 2\n");
return 0;
}
cpu_set_t cpu_info;
CPU_ZERO(&cpu_info);
CPU_SET(0, &cpu_info);
if (0!=pthread_setaffinity_np(t1, sizeof(cpu_set_t), &cpu_info))
{
printf("error:Thread 1 set affinity failed.\n");
}
CPU_ZERO(&cpu_info);
CPU_SET(1, &cpu_info);
if (0!=pthread_setaffinity_np(t2, sizeof(cpu_set_t), &cpu_info))
{
printf("error:Thread 2 set affinity failed.\n");
}
pthread_join(t1, NULL);//释放线程t1
pthread_join(t2, NULL);//释放线程t2
return 0;
}总结几点:
-
Linux下的cpu亲和度 CPU 亲和性(affinity) 就是进程要在某个给定的 CPU 上尽量长时间地运行而不被迁移到其他处理器的倾向性。Linux 内核进程调度器天生就具有被称为 软 CPU 亲和性(affinity) 的特性,这意味着进程通常不会在处理器之间频繁迁移,windows则不然,如果你的电脑是双核,你会看到两条cpu曲线近似相同,进程几乎被两个cpu均分。 Linux下的cpu亲和度可以参考以下博文,讲的非常清楚 http://www.ibm.com/developerworks/cn/linux/l-affinity.html
-
终端编译出错:undefined reference to’pthread_reate’ 加上-lpthread 如:gcc test.c –lpthread 。若使用IDE Code::Blocks 编译出错则要进行以下设置: Project -> Build options -> Linker settings -> Link libraries 里加上pthread
-
Happy Birthday to「某*」. This is just for you.
【参考文献】《编程之美》
【参考博客】管理处理器的亲和性 http://www.ibm.com/developerworks/cn/linux/l-affinity.html
【参考博客】让CPU占用率曲线听你指挥 http://blog.csdn.net/wesweeky/article/details/6402564
【参考博客】Linux下pthread的线程亲和性研究 http://blog.sina.com.cn/s/blog_6a1837e90100nrlj.html